A little physics

[Abitconfused]

Please review the attached illustration and inform me as to the accuracy of the illustration with regard to the physics of light as it passes through a lens.

[flashback]

I thought it was this:


http://www.passmyexams.co.uk/GCSE/ph...ex-lenses.html

[Tringa]

I agree with Jack. The problem with diagram you have Ed is that the lens does not focus the light. I assume if the lens is made poorly then what the diagram shows could occur. I'm sure others who know more than me will be along soon.

Dave

[Stagecoach]

Ed,

Is this illustration depicting a convex/converging lens?

Grahame

[revi]

Ed's illustration would be wrong for both convex and concave lenses...
And the reasoning behind it seems wrong to me, as well:
according to his reasoning, light coming from one point cannot be focused in one point.
And there's a discontinuity in there as well: either there's a zone on the sensor that gets no light,
or the whole edge would end up in one point.

[ajohnw]

Jack's picture is correct neglecting aberrations. Images of objects are formed by light entering the lens at an angle. To show that Jack's image might show another bundle of rays coming into the lens at an angle such that the "image" is upside down. So if the bundle came in from above the axis of the lens the focal point would be below the one from the central rays.

Only problem is that the angled rays would focus on a curved surface in practice so it may look a little odd.

John
-

[Downrigger]

I think Ed’s picture shows a lens not in focus with its film or sensor, and moreover one with a large circle of confusion. If the (brown rectangle – film-sensor) were moved towards the lens to the center of the diamond formed by light rays in the middle of Ed’s picture, then I think this would depict correct focus, and the distance of the long (vertical) diagonal in the diamond would correspond to the diameter of the circle of confusion for that lens at that aperture. (Maybe?)

[Abitconfused]

OK, perhaps this is a better illustration. However, I still think...that light from the center of the lens moves toward the edges of the sensor. For some reason image upload stopped working...on my computer anyway.

[John Morton]

It looks to me that there is a problem with the accuracy of both Ed's and Jack's diagrams.

In Ed's diagram (the first one), it appears that the effect of the first curved surface of the lens is taken into account, as the light enters the lens; but, not second surface where the light exits the lens.

In Jack's diagram, the effect of both surfaces is averaged together and localized to the center of the lens. Of the two diagrams, Jack's is the most accurate overall.

[Abitconfused]

OK, focused? True??

[xpatUSA]

Ed's second image may have had a different purpose. The text however is just plain wrong!

Ignoring the text, the image appears to be illustrating spherical abberation, a la Wikipedia:



See: https://en.wikipedia.org/wiki/Lens_%28optics%29

Ed's first image does not appear to be illustrating the formation of a focused image on the sensor, unlike this:



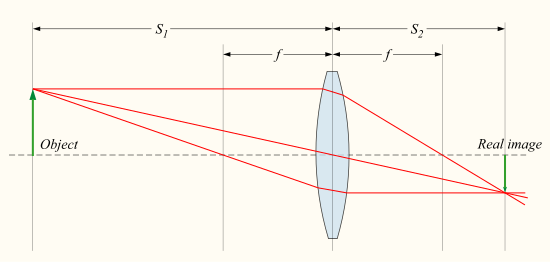
So what was it trying to illustrate?

[ajohnw]

No that isn't correct. The image would be where the rays cross. This explains what happens rather well bearing in mind that all points on the subject emit light rays. Also explains why bigger lenses capture more light.



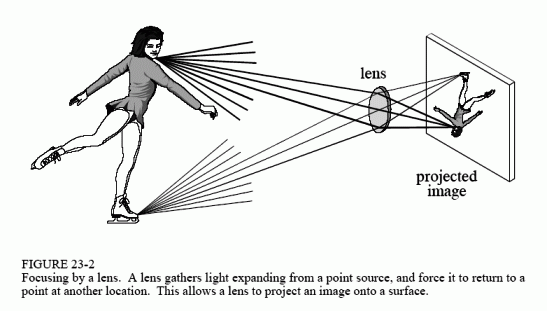
This one shows how to geometrically draw what happens but as above the subject emits rays at more angles than shown. Notice it involves lines passing through the centre of the lens. That's an approximation.



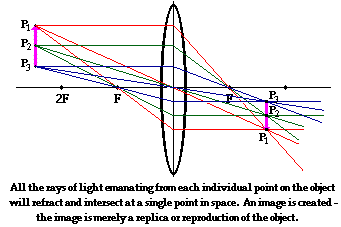
(Yes I do know that the rays from the subject are reflected off it)

John
-

[Inkanyezi]

Ed, f you are not trolling, you probably are more than a bit confused.

A lens, such as used on a camera, will focus an image on the sensor of a camera. Light rays that arrive from one and the same direction, will hit the sensor at one point, its location on the sensor depends on the angle of the incoming light. If light arrives from distant objects, the rays are essentially parallel, and the lens breaks them together, so that they will form an image of the distant object, when the lens is focused at it. A very far away object is regarded as being at "infinity".

For focusing closer, there are two methods, the most easily understood one is moving the lens away, to focus on close objects.

When the lens is focused at infinity, its optical centre is its focal length away from the sensor. When it is focused at a reproduction scale of natural size, 1:1, a common macro scale, the lens' optical centre is two focal lengths away from the sensor, and the object focused upon is four focal lengths away from the sensor.

The other way of focusing is altering the focal length, making it shorter, so that the optical centre stays in more or less the same place, but the focal length of the lens becomes shorter. Effectively it does the same thing as moving the lens away from the sensor, although its angle of view and light gathering power will remain more or less the same. When the lens is moved away, view angle decreases and also the light that falls upon the sensor.

The function of a lens can be explained according to two theories, either wave or ray theory. The result is identical but the theories use different explanations. The wave theory explains it a bit better in my opinion. Light entering an optical denser medium loses speed and the wavelength decreases, while its frequency is the same. The opposite happens when it passes the boundary between the two media in the other direction.

Once you appreciate, that light when it deviates, does not "move" in a direction, but is deflected or deviated, you may understand why a lens will focus rays that arrive parallel, so that it will hit one spot. The rays will deviate more, when they hit the surface of the medium at a more oblique angle.

If nothing here makes sense to you, have another shot and don't worry. Your lens will still make an image.

[xpatUSA]

Please review the attached illustration and inform me as to the accuracy of the illustration with regard to the physics of light as it passes through a lens.

If we are all agreed that the text in above image is pure hogwash, I'll ask again, since Ed did describe the image as an illustration of something, what was that something? Not just "how light rays pass through a lens", surely?

[yauman]

The last diagram from John is the correct one - at least when modeling light rays using geometric optics. Note, that geometric optics is purely a model - a working model, the real physics of light is in it's wave properties. So, I'll try to summarize the 3 "rules" of geometric optics as implemented in a simple "perfect" convex lens (ignoring deviation, aberration etc.)

1. Any rays going through the center point of the lens will not be refracted - it will pass thru unchanged regardless of which direction it came from.
2. Any rays parallel to the axis, after passing through the lens will be refracted to pass through the focal point of the lens (on the other side.)
3. Any rays passing through the focal point will after refraction by the lens emit as rays parallel to the axis of the lens.

With these rules in mind you can set up any Object to Image situation. If the Object is very far away, all rays from it can be considered parallel to axis, so they will all land at the focal point. As the Object closes in, the position of the image will start to move aways from the focal point. You can do the trigonometry and the general lens formula will end up to be the reciprocal equivalence:
1/F = 1/o + 1/i (F= focal length, o=object distance from center of lens, i=image distance from center of lens.)

This all works well for a single color with a simple lens. Since different colors refract differently through the lens, the focal point would be slightly different for blue vs red - thus chromatic aberration and the need for multi-element expensive compound lens.

(It's been many many years since I taught college physics so I won't try to explain the wave equivalent off the top of my head.)

Yau-Man

[Mito]

Please review the attached illustration and inform me as to the accuracy of the illustration with regard to the physics of light as it passes through a lens.

The accuracy of the diagram can at best be called inaccurate. I was always taught that light waves are refracted (bent) through lenses, the amount depending on the design of the lens. In the diagam the light waves at the perifery of the lens will cross and hit the edges of the sensor, the waves passing nearer the centre hitting nearer the centre of the sensor creating an upside down image. The point where the light rays cross is the focal point of the lens. This is the point that Boy Scouts use to light their camp fires. The rest of the world rubs two Boy Scouts together to light their camp fires

[xpatUSA]

This all works well for a single color with a simple lens. Since different colors diffract differently through the lens, the focal point would be slightly different for blue vs red - thus chromatic aberration and the need for multi-element expensive compound lens.

Yes, perhaps the image in the OP was illustrating that difference but with the outside rays being far infrared and the inner ones far UV -

Would still like to know what article that image came. Ed will tell us soon, eh?

[davidedric]

When it comes to this kind of discussion, I think I would always defer to Ted (Xpat USA) .

[MrB]

Yau-Man's description looks OK (Post #15) except that "diffract..." should be "refract...".

Philip

[yauman]

Yau-Man's description looks OK (Post #15) except that "diffract..." should be "refract...".

Philip

Thank you - so corrected (before someone from my alma mata reads it and petition to recall my physics degree